يمكن تعريف البلاطة على سطح الأرض slab-on-grade، والتي تشمل البلاطات الأرضية الصناعية، على أنها بلاطة مدعومة بشكل تام بالأرض بمساحة تزيد عن ضعف المساحة المطلوبة لدعم الأحمال المفروضة. تتمثل أهداف التصميم الأساسية لبلاطة الأرضية الصناعية في حمل الأحمال المقصودة وتجنب تشقق السطح.
قد تكون البلاطة عادية أو مسلحة وقد تشتمل على عناصر تقوية مثل الأعصاب والمخدات المخفية. يمكن توفير التسليح للأغراض الهيكلية أو للتحكم في تأثيرات الانكماش وتغيرات درجة الحرارة.
تعتبر البلاطات الأرضية الصناعية من المكونات الأساسية للمباني الصناعية والمستودعات. لكي تعمل معدات التصنيع والرافعات بشكل صحيح، يجب أن تكون البلاطة مسطحة بشكل موحد ويجب أن تكون المفاصل مستوية نسبيًا دون تحركات مفرطة. وقد استلزم نمو الصناعة استخدام آلات ومرافق تخزين أكبر وأثقل.
بالإضافة إلى ذلك، فإن تطور ممارسات البناء، مثل الاتجاه نحو بلاطات أرضية أكبر مع عدد أقل من المفاصل، واستخدام الأسمنت عالي القوة، والزيادة في استخدام المضافات، كلها ساهمت في زيادة التكسير والتجعيد في هذه البلاطات.
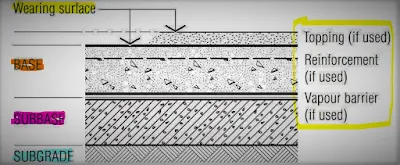
تظهر الصورة التالية الطبقات النموذجية في البلاطة الأرضية الصناعية :
تؤدي الطريقة التي يتم بها تكديس الأحمال الموحدة في المستودعات إلى حدوث بعض التشققات في الممرات بين المناطق المحملة. تنقسم الأنواع السائدة من التشققات في الممرات إلى فئتين. النوع الأول طولي، والثاني عرضي. يعزى التشقق العرضي بشكل مباشر إلى الانكماش، في حين أن التشقق الطولي يحدث نتيجة لطريقة تكديس الأحمال الخارجية في المستودعات.
في المستودعات، يتم عادةً توزيع الأحمال الموحدة الثقيلة على جزء من البلاطة، عادةً حول الأعمدة، مما يترك ممرات واضحة في منتصف هذه الأعمدة.
متطلبات الأرضيات الصناعية الخرسانية
تشمل متطلبات الأرضيات الصناعية الخرسانية ما يلي:
تختلف الاشتراطات التي يجب توفرها للأرضيات الصناعية الخرسانية اعتمادًا على الاستخدام المقصود للأرضية ومتطلبات الموقع. ومع ذلك، يمكن أن تشمل الاشتراطات العامة التالية:
1. سمك الأرضية: يجب أن يتم تحديد سمك الأرضية وفقًا للحمولة المتوقعة وطبيعة العمل المقام على الأرضية. قد تتطلب التطبيقات الصناعية الثقيلة أرضيات خرسانية سميكة تصل إلى 8 بوصات (20 سم) أو أكثر.
2. التسليح: في حالة الأرضيات التي يمكن أن تتعرض لتشققات أو تحركات ، يمكن أن يتم تسليح الأرضية باستخدام شبكة تسليح من الأسلاك الفولاذية المقاومة للصدأ أو إضافة ألياف البوليسترين لتقوية الأرضية.
3. منع تسرب المياه: يجب أن تكون الأرضية خالية من التسرب ، وذلك من خلال استخدام طلاء مانع لتسرب المياه أو طبقة عازلة تحت الأرضية لمنع تسرب الماء.
4. مقاومة التآكل: يجب أن يكون السطح مقاومًا للتآكل والصدمات والمواد الكيميائية ، وذلك باستخدام طلاء خاص أو طبقة حماية لحماية الأرضية من التآكل.
5. تصميم الإضاءة: يجب أن يتم تصميم الأرضية بطريقة تسمح بإضاءة جيدة ومناسبة للمنطقة بأكملها.
6. تنفيذ صحيح: يجب أن يتم تنفيذ الأرضية بواسطة مقاول مؤهل وفقًا للمواصفات والإرشادات الصناعية ذات الصلة.
7. الأخذ في الاعتبار حركة الأرض: يجب أيضا أخذ في الاعتبار حركة الأرض والانتقالات الحرارية عند تصميم البلاطة الأرضية. يمكن استخدام الشروط الجغرافية والجيوتقنية لتخفيض تأثير هذه الحركات على اللوحة.
8. معالجة الضوضاء والاهتزاز: قد يحتاج بعض التطبيقات الصناعية إلى حلول للتحكم في الضوضاء والاهتزاز الناجمة عن عملياتها. يجب أن يتم تضمين هذه الاحتياجات في تصميم واختيار الأرضية الصناعية المناسبة.
يجب مراعاة هذه الاشتراطات ومتطلبات أخرى معممة في المنطقة أو الصناعة المحلية لتحقيق أرضية صناعية قوية وفعالة.
معدات المستودعات وتحميل الأرضيات
تعتبر الأحمال النقطية المركزة من أرفف البليت ومعدات مناولة المواد المصاحبة (MHE) والميزانين بمثابة أحمال متكررة على أرضيات المستودعات. تأتي الأحمال الأخرى من الأحمال الموزعة بشكل موحد (UDL) مثل المنتجات المنقولة على منصات نقالة أو المواد المخزنة السائبة، بالإضافة إلى الأحمال الخطية مثل الجدران الداخلية وأنظمة درابزين الأرضية.
في تصميم البلاطات الأرضية الصناعية، عادة ما تكون الأحمال النقطية هي الأكثر أهمية للتصميم، ولا ينبغي الاعتماد فقط على الأحمال الموزعة بشكل موحد والمحددة بشكل شائع (UDLs). وفي جميع الأحوال يجب أن يعتمد التصميم على الأحمال المتوقعة من جميع أنواع المعدات والأحمال الأخرى، ويجب أن يأخذ المحدد في الاعتبار الاستخدامات المستقبلية المحتملة للأرضية.
ومن المعقول أن نتوقع أن الهياكل الأطول سوف تكون قادرة على دعم أحمال أكبر، مثل تلك التي تفرضها أرفف البليت. يتم التعامل مع الأحمال النقطية من أرفف البليت والميزانين على أنها أحمال ثابتة، في حين يتم التعامل مع المعدات الثقيلة المتنقلة (MHE) على أنها حمل ديناميكي يتطلب عوامل أمان تصميمية أكبر.
تصميم البلاطة الأرضية الصناعية
بالنسبة للأحمال النقطية المركزة الشائعة على بلاطات الطابق الأرضي الصناعية من أرفف التخزين والميزانين ومعدات مناولة المواد (MHE)، هناك وضعان محتملان لفشل القوة النهائي:
- الثني flexure
- الاختراق punching shear
يعتمد تصميم البلاطات تحت الانثناء تحت الأحمال النقطية عند حالة الحد النهائي (ULS) على نظرية خط الخضوع، والتي تتطلب مرونة كافية لافتراض السلوك البلاستيكي.
يؤخذ في الاعتبار أنه سيتم نقل جزء من الحمولة عبر البلاطة إلى الأرض.
يتم تقييم الأحمال الخطية والأحمال الموزعة بشكل موحد باستخدام تحليل مرن يعتمد على Beams on Elastic Foundation الخاصة بـ Hetenyi.
الحد الأدنى الموصى به لسمك البلاطة المدعمة بالأرض هو 150 ملم.
يجب على المصمم أن يأخذ في الاعتبار تقليل السمك الناتج عن استخدام التسليح واستمرارية البلاطة، وغيرها من الميزات.
هناك قيود عملية على كمية الخرسانة التي يمكن صبها في يوم واحد، لذلك تحتوي معظم الأرضيات على وصلات. في معظم الحالات، تكون حالة التحميل الحرجة هي تحميل نقطة قريبة من وصلة البلاطة.
في جميع التصاميم يجب تقييم قدرة تحمل الأرضية إلى جانب الوصلات. ستعتمد هذه القدرة بشكل كبير على قدرة آلية المفصل على نقل الحمل إلى الجانب الآخر من المفصل. وينطبق هذا بشكل خاص على MHE، التي لا يمكن وضعها بعيدًا عن المفاصل، على عكس الأحمال الثابتة.
مثال:
Quadruple Internal Point Loads
Verify the capacity of a 200mm thick concrete industrial ground floor slab subjected to a quadruple internal 300 x 300 point load in accordance with TR34, 4th Edition 2013;
Permanent load; Gk = 45.0 kN
Variable load; Qk = 20.0 kN
Dynamic load; Dk = 30.0 kN
Slab details
Reinforcement type; Fabric
Concrete class; C25/30
Slab thickness; h = 200 mm
Fabric reinforcement type; A393
Characteristic strength of reinforcement; fyk = 500 N/mm2
Area of top steel provided; As,prov = 393 mm2/m
Diameter of reinforcement; fs = 10 mm
Nominal cover; cnom_b = 50 mm
Effective depth of reinforcement; d = 0.75h = 150 mm
Partial safety factors
Concrete (with or without fibre); γc = 1.50
Reinforcement (bar or fabric); γs = 1.15
Permanent; γG = 1.20
Variable; γQ = 1.50
Dynamic loads; γD = 1.60
Subgrade reaction
Modulus of subgrade reaction; k = 0.030 N/mm3
Properties of Concrete
Characteristic compressive cylinder strength; fck = 25 N/mm2
Characteristic compressive cube strength; fcu = 30 N/mm2
Mean value of compressive cylinder strength; fcm = fck + 8 N/mm2 = 33 N/mm2
Mean value of axial tensile strength; fctm = 0.3 N/mm2 × (fck)2/3 = 2.6 N/mm2
Flexural tensile strength; fctd,fl = fctm × (1.6 – h /1000) / γc = 2.4 N/mm2
Design concrete compressive strength (cylinder); fcd = fck / γc = 16.7 N/mm2
Secant modulus of elasticity of concrete; Ecm = 22 kN/mm2 × [fcm/10 ]0.3 = 31 kN/mm2
Poisons ratio; v = 0.2
Radius of relative stiffness (Eqn. 20); l = [Ecmh3 / (12(1 – v2) × k)]0.25 = 924 mm
Characteristic of system (Eqn. 33); l = (3k / (Ecmh3))0.25 = 0.773 m-1
Moment capacity
Negative moment capacity (Eqn. 2); Mn = Mun = fctd,fl × (h2/6) = 16.0 kNm/m
Positive moment capacity (Eqn. 2); Mp = Mun = 16.0 kNm/m
Loading – Quadruple internal 300 x 300 point load
Loading length; ll = 300mm
Loading width; lw = 300mm
Distance x; x = 1000mm
Distance y; y = 1000mm
Permanent load; Gk = 45.0 kN
Variable load; Qk = 20.0 kN
Dynamic load; Dk = 30.0 kN
Contact radius ratio
Equivalent contact radius ratio; a = [(ll × lw) / π]0.5 = 169.3 mm
Radius ratio; a/l = 0.183
Ultimate capacity under single internal concentrated loads
For a/l equal to 0 (Eqn. 21); Pu_0 = 2π(Mp + Mn) = 200.6 kN
For a/l equal to 0.2 (Eqn. 22); Pu_0.2 = 4π(Mp + Mn) / [1 – (a / (3 × l))] = 427.2 kN
Thus for a / l equal to 0.183; Pu = min(Pu_0.2, Pu_0 + (Pu_0.2 – Pu_0) × (a / (l × 0.2))) = 408.2 kN
4 No. individual; Pu_4x1 = 4Pu = 1632.6 kN
Ultimate capacity under dual internal concentrated loads
For a/l equal to 0 (Eqn. 27); Pu_0 = [2π + (1.8 × min(x, y) / l)] × [Mp + Mn] = 262.7 kN
For a/l equal to 0.2 (Eqn. 28);Pu_0.2 = [4π / (1 – (a / (3 × l))) + 1.8 × min(x, y) / (l – (a/2))] × [Mp + Mn] = 495.7 kN
Thus for a / l equal to 0.183; Pu = min(Pu_0.2, Pu_0 + (Pu_0.2 – Pu_0) × (a / (l × 0.2))) = 476.1 kN
2 No. dual; Pu_2x2 = 2 × Pu = 952.2 kN
Ultimate capacity under quadruple internal concentrated loads
For a/l equal to 0 (Eqn. 29); Pu_0 = [2π + 1.8 × (x + y) / l] × [Mp + Mn] = 324.9 kN
For a/l equal to 0.2 (Eqn. 30); Pu_0.2 = [4π / (1 – (a / (3 × l))) + 1.8(x + y) / (l – (a / 2))] × [Mp + Mn] = 564.1 kN
Thus for a / l equal to 0.183; Pu = min(Pu_0.2, Pu_0 + (Pu_0.2 – Pu_0) × (a / (l × 0.2))) = 544.0 kN
quadruple;Pu_1x4 = Pu = 544.0 kN
Ultimate load capacity for 4 No. loads; Pu = min(Pu_4x1, Pu_2x2, Pu_1x4) = 544.0 kN
Check ultimate load capacity of slab
Number of loads; N = 4
Loading applied to slab; Fuls = N × [(GkγG) + (QkγQ) + (DkγD)] = 528.0 kN
Utilisation; Fuls / Pu = 0.971
PASS – Total slab capacity exceeds applied load
Punching shear at the face of the loaded area
Shear factor; k2 = 0.6(1 – fck / 250 N/mm2) = 0.54
Length of perimeter at face of loaded area; u0 = 8 (ll + lw) = 4800 mm
Shear stress at face of contact area; vmax = 0.5k2fcd = 4.500 N/mm2
Maximum load capacity in punching; Pp,max = vmax × u0 × d = 3240.0 kN
Utilisation; Fuls / Pp,max = 0.163
PASS – Total slab capacity in punching at face of loaded area exceeds applied load
Punching shear at the critical perimeter
Shear factor; ks = min(1 + (200mm / d)0.5, 2) = 2.00
Minimum shear stress at 2d from face of load; vRd,c,min = 0.035ks3/2 × (fck)0.5 = 0.495 N/mm2
Ratio of reinforcement by area in x-direction; rx = As,prov / d = 0.00262
Ratio of reinforcement by area in y-direction; ry = As,prov / d = 0.00262
Reinforcement ratio; r1 = (rx × ry)0.5 = 0.00262
Maximum shear stress at 2d from face of load; vRd,c = max(0.18 × ks / γc × (100 × r1 × fck )1/3, vRd,c,min) = 0.495 N/mm2
Length of perimeter at 2d from face of load; u1 = 2 × (lw + y + ll + x + 2π × d) = 7085 mm
Max. load capacity in punching at 2d from face; Pp = vRd,c × u1 × d = 526.0 kN
Ground reaction (cl.7.10.2); Rp = 1.4 × (d / l)2 × Fuls + 0.47 × (ll + x + lw + y) × d × Fuls / l2 = 132.9 kN
Total imposed shear load; Fuls_total = Fuls – Rp = 395.1 kN
Utilisation; Fuls_total / Pp = 0.751
PASS – Total slab capacity in punching at 2d from face of loaded area exceeds applied load
Design Summary
Description Unit Provided Required Utilisation Result
Slab capacity in flexure kN 544.0 528.0 0.971 PASS
Shear at face kN 3240.0 528.0 0.163 PASS
Shear at 2d kN 526.0 395.1 0.751 PASS
Uniformly Distributed Load
Verify the capacity of a 150mm thick concrete industrial ground floor slab to support a uniformly distributed load of 45 kN/m2 in accordance with TR34, 4th Edition 2013;
Slab details
Reinforcement type; Fabric
Concrete class; C25/30
Slab thickness; h = 150 mm
Fabric reinforcement type; A252
Characteristic strength of reinforcement; fyk = 500 N/mm2
Area of top steel provided; As,prov = 252 mm2/m
Diameter of reinforcement; fs = 8 mm
Nominal cover; cnom_b = 50 mm
Effective depth of reinforcement; d = 0.75 × h = 112 mm
Partial safety factors
Concrete (with or without fibre); γc = 1.50
Reinforcement (bar or fabric); γs = 1.15
Permanent; γG = 1.20
Variable; γQ = 1.50
Dynamic loads; γD = 1.60
Subgrade reaction
Modulus of subgrade reaction; k = 0.030 N/mm3
Strength properties for concrete
Characteristic compressive cylinder strength; fck = 25 N/mm2
Characteristic compressive cube strength; fcu = 30 N/mm2
Mean value of compressive cylinder strength; fcm = fck + 8 N/mm2 = 33 N/mm2
Mean value of axial tensile strength; fctm = 0.3 N/mm2 × (fck)2/3 = 2.6 N/mm2
Flexural tensile strength; fctd,fl = fctm × (1.6 – h / 1000) / γc = 2.5 N/mm2
Design concrete compressive strength (cylinder); fcd = fck / γc = 16.7 N/mm2
Secant modulus of elasticity of concrete; Ecm = 22 kN/mm2 × [fcm/ 10 ]0.3 = 31 kN/mm2
Poisons ratio; v = 0.2
Radius of relative stiffness (Eqn. 20); l = [Ecm × h3 / (12 × (1 – n2) × k)]0.25 = 745 mm
Characteristic of system (Eqn. 33); l = (3 × k / (Ecm × h3))0.25 = 0.959 m-1
Moment capacity
Negative moment capacity (Eqn. 2); Mn = Mun = fctd,fl × (h2 / 6) = 9.3 kNm/m
Positive moment capacity (Eqn. 2); Mp = Mun = 9.3 kNm/m
Load 1 – UDL 45 kN/m2
Working load capacity of UDL
UDL; Uk = 45.0 kN/m2
Critical aisle width; lcrit = π / (2 × l) = 1637 mm
Loaded width of single UDL (max positive moment); lload_p = π / (2 × l) = 1637 mm
Loaded width of dual UDL (max nagative moment); lload_n = π / l = 3275 mm
Working load capacity of slab; q = 5.95 × l2 × Mn = 50.9 kN/m2
Utilisation; Uk / q = 0.884
PASS – Total slab capacity exceeds applied load
Design Summary
Description Unit Provided Required Utilisation Result
Slab capacity in flexure kN/m2 50.9 45.0 0.884 PASS